Sie wollen mehr über Euler Math Toolbox erfahren? In diesem Arbeitsblatt (Notebook) möchte ich Ihnen zeigen, wie einfach es ist, in Euler numerische und algebraische Ergebnisse zu erhalten, diese Ergebnisse graphisch aufzubereiten, im Web zu publizieren oder auszudrucken.
Die Sprache von Euler ist eigentlich Englisch. Aber es gibt neben dieser Einführung einige Notebooks, die in deutscher Sprache gehalten sind. Vielleicht haben Sie auch Lust, an der Entwicklung von Euler mitzuwirken und eigene Dokumentationen beizusteuern.
Ich starte mit einer einfachen Aufgabe: Wie lange fällt ein Körper aus 10 Metern Höhe bis zum Boden ohne Berücksichtigung von Luftwiderstand?
>h:=10; g:=gearth$; sqrt(2*h/g)
1.42808698123
Diese Kommandozeile besteht aus
Zur Definition Variablen habe ich ":=" verwendet. Es geht auch nur mit "=". Der Strichpunkt sorgt dafür, dass der Wert der Zuweisung nicht gedruckt wird.
Ich habe hier die Formel für die Fallhöhe
![]()
im Kopf nach t aufgelöst. Die Konstante gearth$ ist in Euler enthalten, zusammen mit vielen anderen Konstanten, deren Namen alle auf $ enden.
>gearth$
9.80665
Wir wollen die Fallzeit graphisch darstellen. Die Funktion plot2d akzeptiert Funktionen oder Ausdrücke in der Variablen x. Ein Ausdruck wird dabei einfach in einer Zeichenkette "..." geschrieben.
Eine Funktion wie plot2d bekommt ihre Parameter mit Komma getrennt. Der erste Parameter ist der Ausdruck, der geplottet werden soll. der zweite und dritte Parameter sind die Grenzen für x. Einige Parameter sind Zuweisungen mit name=wert. Zum Beispiel wird der Label der x-Achse mit xl="h" angegeben.
>plot2d("sqrt(2*x/g)",0,50,xl="h",yl="t",title="Fallzeit"):
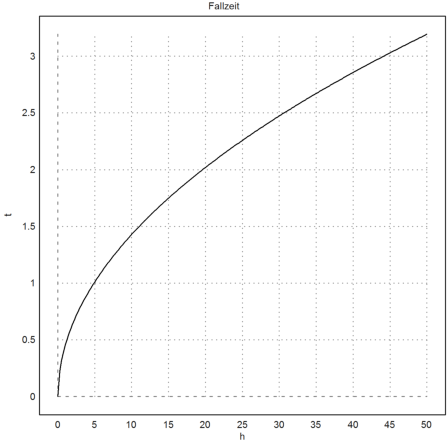
Beachten Sie den Doppelpunkt am Ende der Befehlszeile! Dadurch wird die Grafik aus dem Grafikfenster in das Textfenster eingefügt. Sie erscheint auch nachher bei einem Export des Arbeitsblatts nach HTML.
Das Grafikfenster ist per Default exakt als quadratisch fixiert. Sie können das im Menü für die Grafikoptionen ändern. Dann kann das Fenster auch andere Formate darstellen. Es gibt auch den Befehl aspect(), der das Format ändert. Mehr dazu erfahren Sie im Tutorial über das Plotten.
Das Grafikfenster kann auch versteckt werden (Ctrl-G). Es wird dann nur beim Druck auf die Tabulatortaste angezeigt.
Euler kann Einheiten umrechnen. Die Ergebnisse sind dann stets im Standard System, also in diesem Fall in Sekunden.
>h=30ft; g=gearth$; sqrt(2*h/g)
1.36559767512
Hier ist ein anderes Beispiel mit Einheiten. Sie beobachten einen Turm in 1.2 km Entfernung und messen dessen Winkelhöhe als 2.3 Grad. Wie hoch ist der Turm?
Zum Drucken verwende ich die Funktion print mit einer Nachkommastelle und gebe die auszugebende Einheit an.
>print(1.2km*tan(2.3°),1,unit="m")
48.2m
Sie können selbst neue Funktionen definieren. Als Beispiel definieren wir die Funktion
![]()
>function f(x) := x^3*(ln(x)+1);
Diese Funktion kann nun wie eine eingebaute Funktion verwendet werden.
>f(0.8)
0.397750501727
Die Funktion plot2d kann Funktionen anstatt mit "f(x)" auch einfach mit dem Funktionsnamen plotten.
>plot2d("f",0,0.5):
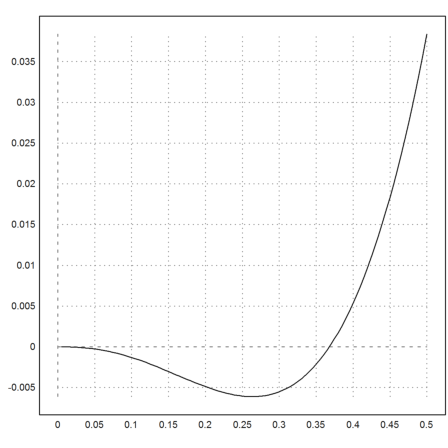
Die Funktion ist lediglich eine numerische Funktion. Um sie zu integrieren oder f(x)=c zu lösen, benötigen wir numerische Methoden.
Im Beispiel ermitteln wir die Nullstelle von f(x) und integrieren von 0 bis zu dieser Nullstelle. Die Funktion solve verwendet das Sekantenverfahren von einem gegebenen Startpunkt aus.
>x0=solve("f",0.35), integrate("f",0,x0),
0.367879441171 -0.00114472743797
Wie wir im nächsten Abschnitt sehen werden, ist es in diesem Beispiel möglich, ein exaktes, symbolisches Ergebnis zu erhalten.
Im folgenden Beispiel ist das nicht möglich. Die numerischen Verfahren von Euler ermitteln aber ein genaues angenähertes Ergebis.
>integrate("sin(x)/x",pi,2pi)
-0.43378547585
Auch für unser erstes Beispiel ist es nicht mehr möglich, die Gleichung f(x)=0.5 symbolisch zu lösen. Aber numerisch geht das sehr gut.
Man kann einfach solve("f(x)-0.5",1) verwenden oder mit y= den Zielwert eingeben. Zum Test berechnen wir f(%), wobei sich % immer auf den letzten berechneten Wert bezieht.
>solve("f",1,y=0.5), f(%)
0.844303665476 0.5
Euler wird zusammen mit Maxima installiert. Das ist ein sehr mächtiges Algebra-Programm, mit dem man Differenzieren, Integrieren, Gleichungen lösen und vieles mehr kann.
Euler verwendet Maxima am einfachsten in Form von symbolischen Ausdrücken. Diese Ausdrücke werden mit & eingeleitet.
>&1/2*g*t^2
2
g t
----
2
Wie man sieht, werden symbolische Ausdrücke in Gleichungsform gedruckt. Das macht Maxima.
Um diesen Ausdruck zum Beispiel nach t aufzulösen, verwendet man solve. Beachten sie, dass es &solve... heißt. Damit wird der ganze Ausdruck symbolisch ausgewertet.
>&solve(1/2*g*t^2=h,t)
h h
[t = - sqrt(2) sqrt(-), t = sqrt(2) sqrt(-)]
g g
Maxima gibt eine Liste von Lösungen aus.
Man braucht die Lösungen nicht abzuschreiben. Es gibt eine Reihe von Techniken, um die Funktionen auszuwerten. Im Beispiel berechnen wir t mit der zweiten Lösung. Dazu definiert man eine symbolische Variable sol, die man dann verwenden kann.
>sol &= solve(1/2*g*t^2=h,t); &t with sol[2]
h
sqrt(2) sqrt(-)
g
Um Ihnen das Beispiel mit der Funktion f aus dem letzten Abschnitt vorzuführen, definieren wir eine symbolische Funktion mit &=. Solche Funktionen können numerisch oder symbolisch verwendet werden.
>function f(x) &= x^3*(ln(x)+1)
3
x (log(x) + 1)
Maxima gibt den natürlichen Logarithmus als log aus. Die Nullstellen berechnet man leicht mit dem symbolischen Solver.
>&solve(f(x)=0,x)
- 1
[x = E , x = 0]
Die Stammfunktion ist ebenfalls exakt darstellbar. Wenn man sie faktorisiert, bekommt man eine schönere Darstellung.
>&integrate(f(x),x), &factor(%)
4 4
x (4 log(x) - 1) x
----------------- + --
16 4
4
x (4 log(x) + 3)
-----------------
16
Hier ist das exakte Ergebnis des Integrals.
>&integrate(f(x),x,0,1/E)
- 4
E
- ----
16
Wie kann man dieses exakte Ergebnis nun berechnen, ohne es abzuschreiben? In Euler geht das einfach dadurch, dass man den symbolischen Ausdruck mit expr() numerisch auswertet.
>expr &= integrate(f(x),x,0,1/E); expr()
-0.00114472743055
Vergleichen Sie das Ergebnis mit dem numerischen Algorithmus. Beachten Sie, dass &f(x) ein symbolischer Ausdruck ist. Damit können die numerischen Algorithmen umgehen.
>integrate(&f(x),0,1/E)
-0.00114472743797
Der Versuch f(x)=1/2 symbolisch zu lösen scheitert. Numerisch lässt sich aber sehr wohl eine Lösung berechnen.
>&solve(f(x)=1/2,x), solve(&f(x),1,y=1/2)
3 1
[x = ------------]
2 log(x) + 2
0.844303665476
Neben der symbolischen Rechnung besitzt Maxima auch Rechnungen mit größerer, im Prinzip unendlicher Genauigkeit.
>&200!/(100!)^2
90548514656103281165404177077484163874504589675413336841320
Im numerischen Teil von Euler steht hier nur die interne 16-stellige Genauigkeit zur Verfügung.
>longest bin(200,100)
9.054851465610333e+058
Zur Demonstration der internen Genauigkeit von Euler ändern wir das Ausgabeformat für einen Moment auf die maximale Länge.
>longest sqrt(2)
1.414213562373095
Dies ist dieselbe Arithmetik wie mit float in Maxima.
>&float(sqrt(2))
1.414213562373095
Es handelt sich um eine IEEE-double-Arithmetik mit Gleitkommazahlen und circa 16 Dezimalstellen.
Maxima besitzt ein Format mit mehr Dezimalstellen, dass allerdings sehr viel langsamer ist. Die genaue Stellenzahl steht in der Variablen fpprec. "bfloat" steht für "big float".
>fpprec&=50; &bfloat(sqrt(2))
1.414213562373095048801688724209698078569671875377b0
Am besten versteht man die Art, wie Euler Numerisches und Symbolisches verwaltet, indem man sich Maxima als separate Welt vorstellt mit eigenen Variablen und Funktionen.
Wenn Funktionen mit := oder Variablen mit = (oder auch :=) definiert werden, so sind sie numerisch und nur in Euler vorhanden.
>anum := 5; function fnum(x) := x^3;
Die beiden Dinge sind in der symbolischen Welt von Maxima nicht vorhanden. Sie werden als undefinierte Ausdrücke behandelt.
>&anum, &fnum(5)
anum
fnum(5)
Wenn man aber Ausdrücke mit &= und Funktionen mit &= definiert, so sind sie in beiden Welten vorhanden.
>asymb &= x^4+x^3; function fsymb(x) &= x^4+x^3;
Die symbolische Auswertung funktioniert wie erwartet in anderen symbolischen Ausdrücken.
>&diff(asymb,x), &fsymb(x+1)
3 2
4 x + 3 x
4 3
(x + 1) + (x + 1)
Numerisch kann man den Ausdruck "asymb" auch auswerten, ebenso wie die Funktion "fsymb", aber nur für numerisches x.
>asymb(0.5), fsymb(0.5)
0.1875 0.1875
Das die Auswertung von Ausdrücken so einfach funktioniert, liegt daran, dass Ausdrücke in x in Euler wie Funktionen ausgewertet werden.
Manchmal will man eine Zahl als numerischen Wert in Euler und Maxima definieren. Das geht mit ::= (oder &:=).
>anumsymb &:= 5.5;
Die numerische Auswertung ist wie gewohnt. Die symbolische Auswertung wandelt in Brüche um.
>anumsymb^2, &anumsymb^2
30.25
121
---
4
Genauso kann man einen Ausdruck oder eine Funktion nur symbolisch definieren.
>asymbonly &&= x^3+x; function fsymbonly(h,x) &&= diff(h,x)
diff(h, x)
Die numerische Auswertung dieser Variablen und Funktionen scheitert. Sie lassen sich nur symbolisch verwenden.
Die Funktion fsymbonly() wirkt praktisch wie ein Makro. Sie differenziert h nach x, wenn sie aufgerufen wird.
>&asymbonly, &fsymbonly(t^3+t,t)
3
x + x
2
3 t + 1
Euler basiert auf einer Matrixsprache genau wie Matlab. Die Grundidee ist:
"Jede Funktion wird elementweise auf Matrizen und Vektoren angewendet."
Wir geben einen Vektor elementweise ein.
>v=[4,5,2,3,9,10]
[4, 5, 2, 3, 9, 10]
Alle Funktionen werden elementweise auf v angewendet.
>sqrt(v)
[2, 2.23607, 1.41421, 1.73205, 3, 3.16228]
Auch alle Operatoren werden elementweise angewendet.
>v*v
[16, 25, 4, 9, 81, 100]
Dies ist nicht das Skalarprodukt. Für das Skalarprodukt verwendet man die Funktion scalp.
>scalp(v,v)
235
Für das Matrixprodukt kann man auch den Punkt . verwenden. Mit dem transponierten Vektor v' kann man das Skalarprodukt dann ebenfalls berechnen.
>v.v'
235
Man beachte, dass v ein Zeilenvektor ist.
Multipliziert man v mit einer Zahl, so wird auch das elementweise durchgeführt.
>2*v, v*2
[8, 10, 4, 6, 18, 20] [8, 10, 4, 6, 18, 20]
Matrizen definiert man zeilenweise.
>A = [1,2,3;4,5,6;7,8,9]
1 2 3
4 5 6
7 8 9
Auch dafür gilt der Grundsatz der elementweisen Evaluation.
>A*A
1 4 9
16 25 36
49 64 81
Das Matrixprodukt wird mit . berechnet.
>A.A
30 36 42
66 81 96
102 126 150
Die inverse Matrix wird mit inv berechnet.
>inv([1,2,3;4,5,6;7,8,10])
-0.666667 -1.33333 1
-0.666667 3.66667 -2
1 -2 1
So eine Matrix kann man auch als Bruch ausgeben.
>fraction inv([1,2,3;4,5,6;7,8,11])
-7/6 -1/3 1/2
1/3 5/3 -1
1/2 -1 1/2
Es gibt viele Funktionen aus der linearen Algebra.
>det(A)
0
>w=kernel(A)
1
-2
1
>eigenvalues(A)
[ 16.1168+0i , -1.11684+0i , 0+0i ]
Der Zweck der Matrixsprache liegt aber in Erstellen von Funktionstabellen.
Wir erzeugen einen Vektor mit Werten.
>k=0:10
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Dazu die Auswertung einer Funktion an diesen Werten mit
![]()
>b=bin(10,k)
[1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1]
Dann können wir das Ergebnis sehr leicht plotten. Wir plotten alles gleich zweimal. Einmal als Streckenzug, einmal als Punkte.
>plot2d(k,b); plot2d(k,b,>points,>add):
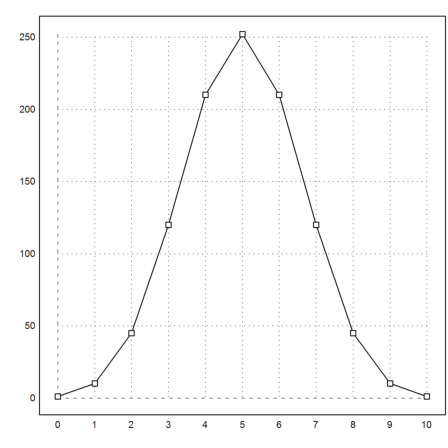
Auch Plotroutinen aus der Statistik können Vektoren in verschiedener Art und Weise darstellen.
>columnsplot(b,lab=0:10):
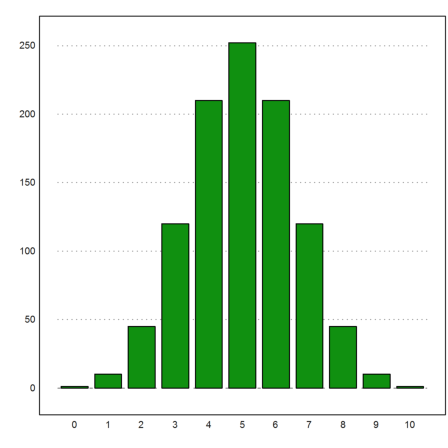
In Maxima lassen sich symbolische Matrizen definieren.
>A &= [1,2,3;4,5,6;7,8,x]
[ 1 2 3 ]
[ ]
[ 4 5 6 ]
[ ]
[ 7 8 x ]
Davon kann man die Determinante berechnen, und etwa det(A)=0 lösen.
>&det(A)|ratsimp, &solve(det(A)=0,x)
27 - 3 x
[x = 9]
Hier sind die exakten Eigenwerte für den Fall x=9, einschließlich ihrer Vielfachheit.
>&eigenvalues(A with x=9)
15 - 3 sqrt(33) 3 sqrt(33) + 15
[[---------------, ---------------, 0], [1, 1, 1]]
2 2
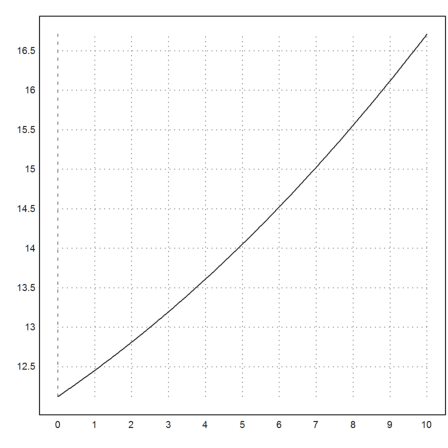
Wir können auch eine Funktion erzeugen, die den Spektralradius in Abhängigkeit von x berechnet.
>function rho(x) := max(abs(eigenvalues([1,2,3;4,5,6;7,8,x]))); ...
plot2d("rho",0,10):
Die Beispiele und die Dokumentation von Euler sind, wie gesagt, überwiegend in Englisch. In Deutsch gibt es nur einige Beispiele. Herr Gellißen hat ein deutsches Handbuch für Euler geschrieben, das Sie im Nezt finden.
Falls Sie an Numerik interessiert sind finden Sie mit dem folgenden Link ein Skript über Numerik, das Euler verwendet.